最近一段时间一直在刷力扣题,除参加字节的七天刷题挑战之外,其它时间大体按照算法模板分类型训练。
开头的二叉树、链表、栈和队列三节基本没有遇到什么问题,如今来到了二进制小节。因为之前了解较少的缘故,我做这一类题目已经沦落到了每道题都要看题解的地步(悲)。于是打算写篇博文记录一下每道题目的思路,方便自己以后回顾。
136. 只出现一次的数字#
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
利用位运算的性质,0^a=a,a^a=0,所以使用初始的 0 将数组遍历异或,最后剩下的即为只出现一次的元素。
package main
func singleNumber(nums []int) int {
result := 0
for _, value := range nums {
result ^= value
}
return result
}
137. 只出现一次的数字 2#
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现三次。找出那个只出现了一次的元素。
这道题目比起上一道,虽然只做了一点改动,但难度显著上升。
先回顾一下上一道题的思路:我们选择对数组进行遍历异或,是因为异或运算能保证对同一元素计算两次后能够返回初始状态,即0=0^a^a。而这道题目中重复元素出现了三次,参照上一道题的思路,我们希望找到一种运算 @,对于任意数 a,使得:0 = 0@a@a@a。
进一步阐述上一道题的情况,设数字被记录下来为 1,数字未被记录为 0, 通过异或运算,我们满足了:

因此出现两次的数字全部被抵消,最后剩下的是出现一次数字的记录状态,即为结果。
对于二进制数字,每位只能表示两个状态,不适用于我们的情况,因此我们可以考虑使用两位二进制来表示结果中的某一位,从 00 出发,在遇到 3 次 a 后返回 00 状态。
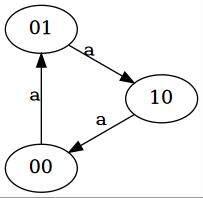
使用两个变量表示这两位(依次为 x、y),我们要求当且仅当第二次遇到 a 时,x 为 0^a;当且仅当第一次遇到 a 时,y 为 0^a。这样即可最终抵消出现三次的数字,最后会处于 01 状态,此时 y 为结果。
package main
func singleNumber(nums []int) int {
var x, y int
for _, value := range nums {
y = (y ^ value) & ^x
x = (x ^ value) & ^y
}
return y
}
260. 只出现一次的数字 3#
给定一个非空整数数组,除了两个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
设两个只出现一次的元素为 a、b。使用第一题的思路,我们可以很轻松地求得 a^b 的结果,但如何分别求出来 a 和 b 呢?
考虑 a^b 的二进制表示中结果为 1 的位,这位为 1 说明 a 和 b 在该位的数值不同,通过利用结果为 1 的位,我们可以将 a 和 b 区分到两个不同的组。而因为其它数都刚好出现两次,故它们必定会成对被分配到同一个组中。这样两个组都相当于第一题,分别求解即可。
注:要看懂以下代码,你需要知道:
- n&(n-1) 可以去掉 n 的二进制表示中最后一位 1。
- (n&(n-1))^n 可以得到 n 的二进制表示中最后一位 1。
package main
func singleNumber(nums []int) []int {
var diff int
for _, value := range nums {
diff ^= value
}
// 设结果为a、b,当前得到的diff是a^b的结果
// 取到diff的任意一位1(此处使用的是最后一位)
diff = (diff & (diff - 1)) ^ diff
result := []int{0, 0}
for _, value := range nums {
if value&diff == 0 {
result[0] ^= value
} else {
result[1] ^= value
}
}
return result
}
191. 位 1 的个数#
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 '1' 的个数(也被称为汉明重量)。
过于简单,不断按位与并将参数右移,计算 1 的个数即可。
func hammingWeight(num uint32) int {
var count int
for num != 0 {
count += int(num & 1)
num >>= 1
}
return count
}
338. 比特位计数#
给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ,计算其二进制数中的 1 的数目并将它们作为数组返回。
这道题的简单思路是遍历 i,对每个 i 使用上一道题目的算法,但复杂度太高。为了简单,我们可以使用动态规划,只需找到递推关系即可。
设数 i 中出现二进制数 1 的个数为 f (i)。
第一种递推关系,显而易见,数 i 中出现二进制数 1 的个数等于 i 右移一位的数中出现二进制数 1 的个数加上 i 的二进制表示中最后一位的值。例如:
3 二进制表示为11
1 二进制表示为1
f(3)=f(1)+1
---------------------------
4 二进制表示为100
2 二进制表示为10
f(4)=f(2)+0
第二种递推关系其实同样简单,数 i 中出现二进制 1 的个数等于 i 的二进制表示中移除最后一位 1 后的数中出现二进制 1 的个数加上 1。例如:
3 二进制表示为11
2 二进制表示为10
f(3)=f(2)+1
---------------------------
4 二进制表示为100
0 二进制表示为000
f(4)=f(0)+1
二进制表示中移除最后一位 1 的方式已经在只出现一次的数字 3中提到过。
package main
func countBits(num int) []int {
result := make([]int, num+1)
for i := 1; i <= num; i++ {
result[i] = result[i>>1] + (i & 1)
// 或者result[i] = result[i & (i-1)] + 1
}
return result
}